Nech už sa rozhodneme riešiť akúkoľvek situáciu, všade sa vyskytujú nejaké parametre, veličiny v nejakej forme, napr. ceny, najazdených kilometrov, čas čakania, hmotnosť a to všetko navyše za splnenia určitých podmienok. Tieto veličiny predstavujú nejaké čísla, hodnoty. Tieto hodnoty potom ďalej analyzujeme. Od prvopočiatkov matematiky vzniklo pomerne dosť disciplín zaoberajúcich sa analyzovaním alebo ešte lepšie povedané optimalizovaním rôznych úloh. Medzi typické disciplíny, ktoré sa týmto zaoberjú patrí: Lineárne a kvadratické programovanie,Geometrické programovanie, Diskrétne a celočíselné programovanie, Dynamické programovanie a Stochastické programovanie (Teória hromadnej obsluhy). Všetky tieto programovania sú odvetvím matematiky a ako hlavnú metódu používajú derivácie (prvé, druhé, parciálne, tiež gradienty a Hesseho matice). Derivácie ako také je možné použiť aj v iných odvetviach vedy, často vo fyzike, geometrii a technických disciplínach.

Derivácia je dobrá v tom(okrem iného), že nám dokáže povedať niečo o priebehu pôvodnej funkcie. Takže napr. máme funkciu: f(x) = ln(x)/x (na obrázku znázornená červenou farbou). Ona môže predstavovať čokoľvek od rastu cien HDP až po priebeh teploty. Máme potom druhú funkciu, jej deriváciu v tvare: f'(x) = (1 - ln(x))/x^2 (znázornená modrou farbou).

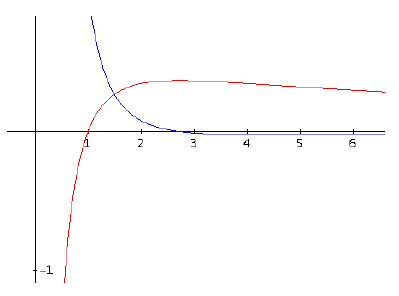
Pôvodná (nederivovaná) funkcia f je rastúca, keď jej derivácia nadobúda kladné hodnoty a klesajúca, keď derivácia nadobúda záporné hodnoty. Bod, v ktorom má funkcia f maximum je v bode, kde je hodnota derivácie nulová. Teda z derivácie je možné vyčítať niektoré informácie o priebehu pôvodnej funkcie.

A teraz ako naprogramovať deriváciu ? Najskôr si ešte zadefinujeme pojem derivácie. Teda, nech funkcia f(x) je definovaná v okolí bodu a. Potom môžme napísať niečo také: lim (f(x) - f(a))/(x-a) = lim (f(a+h) - f(a))/h a túto limitu nazveme deriváciou funkcie f(x) v bode a, čo sa označuje f'(a). (limita x->a)

Príklad: Máme vypočítať deriváciu funkcie f(x) = x^3 v bode a.

f'(a) = lim (x^3 - a^3)/(x - a) = lim (x - a)*(x^2 + a*x + a^2)/(x - a) = lim (x^2 + a*x + a^2) = a^2 + a^2 + a^2 = 3*a^2

Budeme používať nasledujúce hlavičkové súbory:

#include <stdio.h>
#include <conio.h>
#include <math.h>

Zadefinujeme si funkciu f s jedným vstupným parametrom typu float, ktorá vráti hodnotu funkcie typu float v tomto bode:

float f(float x)
{
    return x*x*x;
}

A teraz si definujeme funkciu, ktorá bude počítať, aproximovať, funkciu v bode a:

float prvaDerivacia(float bod)
{
    float xt = bod;
    float h = 0.01 * (1 +  abs(xt));
    bod = xt + h;
    float fp = f(bod);
    bod = xt - h;
    float fm = f(bod);
    bod = xt;
    return (fp - fm)/2/h;
}

A ešte hlavnú funkciu main, ktorá len zavolá funkciu prvaDerivacia a vytlačí výsledok na obrazovku:

void main(void)
{
    printf("%f", prvaDerivacia(2) );
getch();
}

Poznámka: Namiesto pozastavenia obrazovky je možné namiesto getch() použiť aj system("pause"), ale potom treba použiť hlavičkový súbor stdlib.h.
Ak program preložíme a spustíme, vypíše hodnotu 12.000895, čo je približne 12. A skutočne. Funkcia x^3 v bode 2 je 8 a jej derivácia 3*x^2 v bode 2 je 12. Teda naozaj nám funkcia derivuje.